casio 201p program manual

this program library was sold separately in 1977.

the programs formed the basis of a library that casio was to perpetuate in later machines, like the fx-501p, the fx-502p and even the fx-700p. the program stock being supplemented somewhat by more ambitious programs later on.

the programs contained here consist mostly of implementation of simple formulae from maths, physics and chemistry. this is mainly due to the limitations of these machines. the three programmable models were functionally similar as described here by the manual itself.

	fx-201p. standard model, 127 step, fortran method, 10 memory, scientific, mains/battery application.
	fx-202p. delux version of fx-201p. all of the same features, plus one year program protection. separate silver-oxide battery system stores and protects any program for repeated use and against accidental loss.
	pro fx-1. magnetic card version of fx-201p. all features the same. programs can be recorded on credit card sized mag. cards. the logic, features, program length (127 steps), and program method (fortran) are identical on all three models.

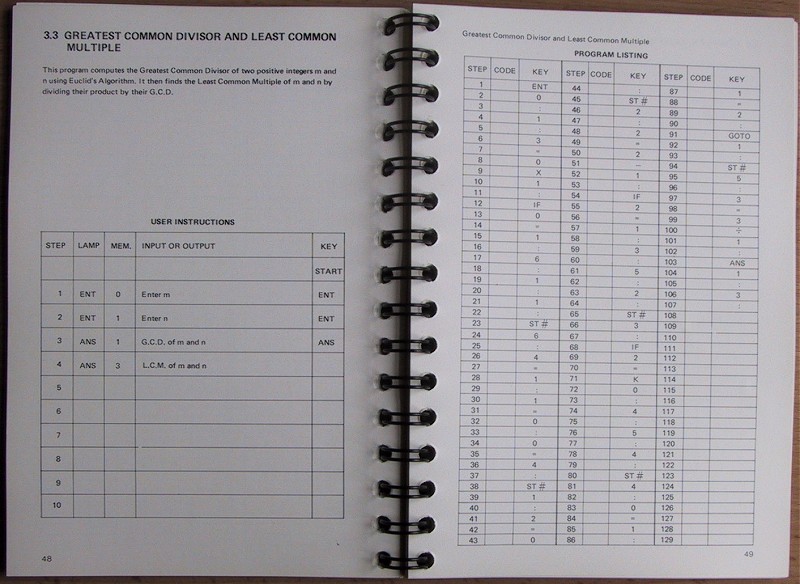
here is the contents page:

unfortunately, the authors of this library didnt really try that hard to write exciting programs for these machines. although i havent been through the details of every single program in this book, i dont think there is one that uses the indirect addressing features of the machine. which means that the manufacturers must have known that this feature was pretty much useless on a machine with such small capacity.

whilst developing my moon phase program, i discovered a rather cunning way to perform mod(x,n) without doing slow and tedious repeated subtraction. the authors could have used this trick to improve the following gcd program reproduced here.

the execution speed of these machines was quite slow, so mod by repeated subtraction was very slow indeed for large numbers. here is a translated version of the above program into `c' code using the same logic.

static float m0,m1,m2,m3,m4,m5,m6,m7,m8,m9;
float gcd0(int a, int b)
{
    m0 = a;
    m1 = b;

    if (m0 < m1) goto st6;
    else if (m0 == m1) goto st1;
    else goto st1;
st6:
    m4=m1;
    m1=m0;
    m0=m4;
st1:
    /* m0 >= m1 */
    m2=m0;
st2:
    m2=m2-m1;
    if (m2 < m1) goto st3;
    else if (m2 == m1) goto st5;
    else goto st2;
st3:
    if (m2 < 0) goto st4;
    else if (m2 == 0) goto st5;
    else goto st4;
st4:
    m0 = m1;
    m1 = m2;
    goto st1;
st5:
    return m1;
}

i know this program looks horrible, but it shows the exact same form of logic as the 201 program including the weird 3-way branches expressed here by if..else..else

ok, i dropped the lcm bit from the book above, since this is just m0*m1/gcd(m0,m1).

now consider the saving if an INT instruction were present,

#define INT(_x)         floor(_x)
float gcd1(int a, int b)
{
    m0 = a;
    m1 = b;

    m2=m0;
    if (m0 < m1) goto st6;
    else if (m0 == m1) goto st5;
    else goto st1;
st6:
    m0=m1;
    m1=m2;
st1:
    /* m0 >= m1 */
    m2=INT(m0/m1)*m1;
    m2=m0-m2;
    if (m2 < 0) goto st5;
    else if (m2 == 0) goto st5;
    else goto st6;
st5:
    return m1;
}

mod(m0,m1) is performed by m0-int(m0/m1)*m1.

also, if m0==m1 we can stop with m1, unlike the original.

and the st4 swap has been merged with st6.

here is the above translated into 201p

ENT 0 : 1 : 9 = K 1 0 10^x : 2 = 0 : IF 0 = 1 : 6 : 5 : 1 :
ST# 6 : 0 = 1 : 1 = 2 : ST# 1 : 2 = 0 / 1 + 9 - 9 * 1 : 2 =
0 - 2 : IF 2 = K 0 : 5 : 5 : 6 : st# 5 : ANS 1 :

Total: 77 steps.

now you can see the INT trick. i put 1e10 into m9 when added and subtracted from a calculation, it has the side effect of displacing any non-integral part off the end of the float precision. it works because the calculator operates internally in decimal to 10 figures.