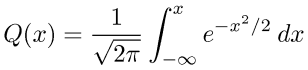hp32e
| the 30 series (spice models) were the third
generation models. this one is a particular favourite of mine, although
not programmable, is a competent and highly usable scientific. the keys
are of high quality with a soft click positive feel to them.
a ten digit led scientific with unit conversions, hyperbolic functions and a rather good set of statistics. it is able to perform 2d stats with linear regression and also normal distribution (the Q function) - and its inverse. the availability of normal probability was (and still is) rare as a keyboard function (eg sharp el-545h, commodore sr9190r) often available as part of a programmable program library. did any other model ever have normal inverse on keyboard? lets take a closer look at the Q function
here is a table of values as calculated by this machine. they are all correct to 10 digits.
|
 |
this accuracy is quite interesting because versions given by program libraries, most often use hasting approximation, which is a polynomial approximation accurate to within 7.5x10^-8 (worst case around 0.717). clearly this model does not use this same approximation internally. hasting approximation is used by the hp29c program library and also turns up in casio models like the fx-201p and later models inheriting the same library.
the inverse operation Q^-1 performs an iteration. you can see the digits dance whilst this calculates for several seconds. it too is accurate.
shown here is how to dismantle a spice calculator.