| i | interest rate | |
| n | number of periods | |
| PMT | periodic payment | |
| PV | present value | |
| FV | future value |
related by the following formula:
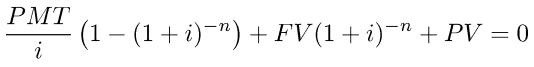
Calculating FV
rearranging the above formula gives the following for FV:
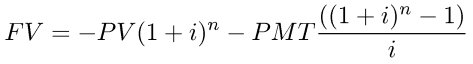
this formula will give correct answers for fv unless i is small in which case there can be problems. in such cases, the formula is numerically unstable because the term (1+i) cannot be accurately accommodated in the computer or calculator precision.
let's take an example (from the hp15c):
an accountant is paid $0.01 per second every day and night for a year. the money is deposited directly into her bank account which pays 10% interest pa compounded every second. what is the correct bank balance after one year?
for this, we have, PV=0, PMT= -0.01, n = 365*24*60*60 and i = 10%/n. plugging the numbers into a 10 digit calculator gives the answer FV = $312,925.02. this answer is wrong!. the reason for the error is that on my calculator 1+i is 1.000000003 and as you can see, almost all of the value of i has been pushed off the edge of 10 digit precision.
how can this be remedied?
one way is to notice that (1+i)^n = e^(n*ln(1+i)). if we had a special kind of log function, ln1(x) = ln(x+1) we can write this as e^(n*ln1(i)). the formula for FV then becomes:
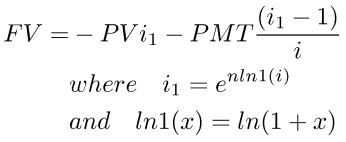
how do we get the ln1(x) function?
some calculators already have this function, models such as the hp41c and the later 48g series for example. another way, suggested by the hp15c advanced functions handbook p181 is as follows,
let u = 1 + x
let ln1(x) = x if u = 1 or ln(u)x/(u-1) otherwise.
the explanation of why this works is in the handbook and it depends on the internal error propagation properties of the machine. i have found it to work on a wide variety of physical calculators, but not for computers.
the other way is to implement ln1(x) manually.
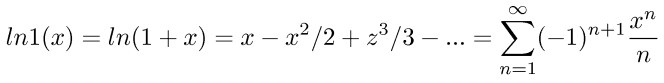
the series will converge for |x| < 1, but we only want it for very small x for which it will converge rapidly. for example we could write a ln1(x) which uses the series when |x| < 0.01 (say) otherwise it returns ln(1+x). something like this:
double ln1(double x)
{
double s = x;
double c = 2;
double t;
double s1; if (fabs(x) >= 0.01) return log(1+x);
x = -x;
t = x;
for (;;) {
t *= x;
s1 = s - t/c;
if (s1 == s) break;
c += 1;
s = s1;
}
return s1;
}
using this approach we can finally get the right answer to the example problem:
ln1(.1/31536000) = 3.170979193348904122791329567241e-9,
i1 = 1.105170917900423925602594466144 and finally
FV = 0.01*(i1-1)/i = 331667.006690776891780341908435
this final answer is given by scicalc with the input fv(.1/31536000,31536000,-0.01,0)
Calculating PMT
from the original formula, rearranging for PMT gives:
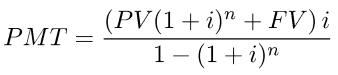
the analysis goes the same as the above for FV, you have to use the ln1(x) trick to calculate (1+i)^n, once this is done, there are no new problems.
Calculating i
this is much more challenging than any of the above problems. firstly, the formula cannot be re-arranged for i explicitly so some kind of iterative method is required for i.
working from the original formula, its derivative can be found and re-arranged so as to include parts of the original as common subexpressions. this will help reduce calculation. we get:
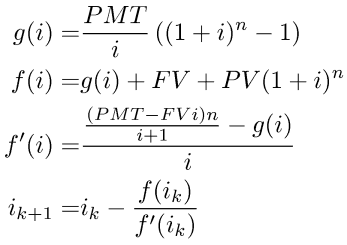
g(i) has been factored out as a common subexpression. again it is necessary to calculate (1+i)^n using the ln1(x) method as described earlier.
the iteration shown with ik follows the usual newton-rapson processes. it only remains to provide some good guesses for the starting value of i. if the guesses are bad, nasty things can happen and this part is quite important. furthermore, the amount of iterative work is vastly reduced if the guesses are sensible.
some sensible guesses can be derived using the idea of calculating the interest payment without compounding. these give the following:
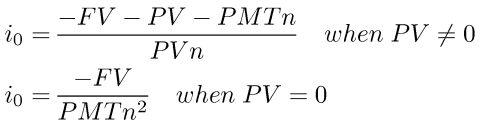
putting these ideas together, here is an example program in C:
double tvmi(double pv, double pmt, double fv, int n)
{
double i;
double i1;
/* iterate to find i given the input values */ /* use guess for i */
if (pv) {
i = (-fv - pv - pmt*n)/pv/n;
}
else {
i = -fv/pmt/n/n;
}
for (;;) {
double t1 = exp(n*ln1(i));
double t2 = pmt/i*(t1-1);
double t3 = t2+fv+pv*t1;
double t4 = (t2+(fv*i-pmt)*n/(1+i))/i;
i1 = i + t3/t4;
if (fabs((i1-i)/i1) < 1e-15) break;
i = i1;
}
return i1;
}
there are more problems with this iterative approach. for example some values are badly conditioned and the calculation can oscillate, never reaching a relative error of 1e-15 (for example), or even any decent relative error.
consider the problem rate(32, 0, -999999,1000000) ie find the interest rate (i) with n = 32, PMT = 0, PV = -999999 and FV = 1,000,000. the above program will not converge and this is due to the A-B problem (ie the subtraction of two very similar numbers pulling out garbage).
for this example, with PMT = 0, the solution is just (-fv/pv)^(1/n)-1. if you try this you will see the badness. what this means is that certain problems, usually involving small i, are badly conditioned and will require extended precision to calculate more accurately. for the above type example, the 1,000,000 will mean something like 6 significant figures are likely to be lost in calculation.
even bearing this in mind, the sort of iteration described above cannot simply continue until epsilon is met, because epsilon might never be met (eg use -9999999 and 10,000,000 and then 7 digits are lost and so on).
the scicalc rate function performs the above algorithm, stopping when the value settles down rather than iterating for a specific relative error.
lets try some examples:
example1:
consider again the example earlier, but this time provide FV and solve
for i. we have:
FV = 331667.006690776891780341908435
n = 365*24*60*60
PV = 0
PMT = -0.01
using scicalc, we get;
i = rate(31536000,-0.01,0,fv(0.1/31536000,31536000,-0.01,0))*31536000
= 1.000000000000000000000000000067e-1 (after 11 iterations).
on the hp12c (a very trusty financial
calculator), we get;
f FIN
31536000 sto 0, n
10 rcl 0 / i
0.01 chs PMT
FV (running=) 331,667.0067 (the correct answer)
then to solve for i, press i (running), then rcl 0 * gives 10.08332639%
which is fairly close (note that scicalc percentages are decimal ie. 0.10 => 10%)
example 2:
lets take the, rather nasty case as follows:
FV = 1,000,000
PV = -999,999
PMT = 0
n = 32
scicalc gives, rate(32,0,-999999,1000000) = 3.125001611329216004244744309188e-8
the correct answer is: 3.1250016113292160042447454442681746383648e-8
so scicalc is incorrect in the last 7 digits. this is to be expected
unless even more precision is used.
for the hp12c,
it goes as follows;
f FIN
32 n
999999 chs PV
1000000 FV
i (running) 3.125004736e-6%
so the 12c gets 6 correct figures which is very good. possibly it has 12 internal digits for these calculations which accounts for the expected loss of 6 figures.